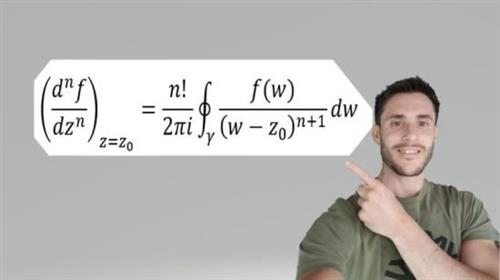Partial Differential Equations – Comprehensive Course

What you'll learn
How to use the Fourier Trasforms to tackle the problem of solving PDE's
Fourier Transforms in one and multiple dimensions
Method of separation of variables to solve the Heat equation (with exercises)
Method of separation of variables to solve the Laplace equation in cartesian and polar coordinates (with exercises)
How to apply the Fourier Transform to solve 2nd order ODE's as well
concept of streamlines
Mathematical tricks
How to derive Heisenberg Uncertainty Principle using concepts of Probability Theory
Requirements
Calculus (especially: derivatives, integrals)
Multivariable Calculus (especially: the Jacobian, the Laplacian, etc.)
Complex Calculus (basics of Fourier series and residues could help)
Some notions of probability theory (distributions, mean, variance)
Complex numbers
Description
Solving Partial Differential Equations using the Fourier Transform: A Step-by-Step GuideCourse Description:This course is designed to provide a comprehensive understanding of how the Fourier Transform can be used as a powerful tool to solve Partial Differential Equations (PDE). The course is divided into three parts, each building on the previous one, and includes bonus sections on the mathematical derivation of the Heisenberg Uncertainty Principle.Part 1: In this part, we will start with the basics of the Fourier series and derive the Fourier Transform and its inverse. We will then apply these concepts to solve PDE's using the Fourier Transform. Prerequisites for this section are Calculus and Multivariable Calculus, with a focus on topics related to derivatives, integrals, gradient, Laplacian, and spherical coordinates.Part 2: This section introduces the heat equation and the Laplace equation in Cartesian and polar coordinates. We will solve exercises with different boundary conditions using the Separation of Variables method. This section is self-contained and independent of the first one, but prior knowledge of ODEs is recommended.Part 3: This section is dedicated to the Diffusion/Heat equation, where we will derive the equation from physics principles and solve it rigorously. Bonus sections are included on the mathematical derivation of the Heisenberg Uncertainty Principle.Course Benefits:Gain a thorough understanding of the Fourier Transform and its application to solving PDE's.Learn how to apply Separation of Variables method to solve exercises with different boundary conditions.Gain insight into the Diffusion/Heat equation and how it can be solved.Bonus sections on the Heisenberg Uncertainty Principle provide a deeper understanding of the mathematical principles behind quantum mechanics.Prerequisites:Calculus and Multivariable Calculus with a focus on derivatives, integrals, gradient, Laplacian, and spherical coordinates.Prior knowledge of ODEs is recommended.Some knowledge of Complex Calculus and residues may be useful.Who is this course for?Students and professionals with a background in Mathematics or Physics looking to gain a deeper understanding of solving PDE's using the Fourier Transform.Those interested in the mathematical principles behind quantum mechanics and the Heisenberg Uncertainty Principle.
Overview
Section 1: Fourier Transform and its inverse
Lecture 1 Fourier series
Lecture 2 Fourier Transforms
Lecture 3 How to interpret improper integrals of sinusoids
Lecture 4 Dirac delta
Lecture 5 Multiple Fourier Transforms
Lecture 6 Why the Dirac delta helps derive the Inverse Fourier Transform
Section 2: Solution of a PDE equation
Lecture 7 Gradient and Laplacian: quick summary
Lecture 8 Example of pde
Lecture 9 Solution to the pde part 1
Lecture 10 Solution to the pde part 2
Lecture 11 Solution to the pde part 3
Section 3: Some more physics behind the pde
Lecture 12 Physics behind the equation part 1
Lecture 13 Physics behind the equation part 2
Section 4: Solving the Diffusion/Heat equation by Fourier Tranform
Lecture 14 Setup of the diffusion problem
Lecture 15 Integral equation satisfied by the function f(x,t)
Lecture 16 Diffusion equation
Lecture 17 Some possible boundary conditions of the diffusion equation
Lecture 18 Solution of the diffusion equation part 1
Lecture 19 Solution of the diffusion equation part 2
Lecture 20 Solution of the diffusion equation part 3
Lecture 21 Solution of the diffusion equation part 4
Section 5: 2nd order ODE solved via Fourier Transform
Lecture 22 2nd order non-homogeneous ODE solved via Fourier Transform
Section 6: PDE solved with the method of characteristics
Lecture 23 Non linear first order PDE solved with the method of characteristics
Section 7: Heat equation solution via Separation of Variables
Lecture 24 Separation of variables to solve the heat equation (part 1)
Lecture 25 Separation of variables to solve the heat equation (part 2)
Lecture 26 Separation of variables to solve the heat equation (part 3)
Section 8: Laplace Equation solved via the method of Separation of Variables
Lecture 27 Laplace Equation in Cartesian Coordinates (exercise)
Lecture 28 Laplace Equation in Polar coordinates (exercise 1)
Lecture 29 Laplace Equation in Polar coordinates (exercise 2)
Lecture 30 Laplace Equation in Polar coordinates (exercise 3)
Lecture 31 Laplace Equation in Polar coordinates (exercise 4)
Lecture 32 Concept of streamlines (with exercise)
Section 9: Nonhomogeneous Heat Equation
Lecture 33 Nonhomogeneous Heat Equation: Exercise 1
Lecture 34 Nonhomogeneous Heat Equation: Exercise 2
Lecture 35 Nonhomogeneous Heat Equation: Exercise 3
Section 10: Wave Equation (Exercises)
Lecture 36 Nonhomogeneous Wave Equation (Exercise 1)
Lecture 37 Nonhomogeneous Wave Equation: D'Alambert formula
Lecture 38 Solving a wave equation using D'Alambert formula (exercise)
Lecture 39 Energy conservation law for the wave equation
Section 11: Bi-dimensional problems (heat and wave equation)
Lecture 40 Bi-dimensional heat equation: exercise 1
Lecture 41 Bi-dimensional heat equation: exercise 2
Lecture 42 Bi-dimensional wave equation: exercise 1
Section 12: Derivation of the Navier-Stokes equations and their solution in a 2D case
Lecture 43 Mathematical derivation of Navier Stokes equations part 1
Lecture 44 Mathematical derivation of Navier Stokes equations part 2
Section 13: How Einstein mastered Navier-Stokes equations in his PhD dissertation
Lecture 45 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 1
Lecture 46 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 2
Lecture 47 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 3
Lecture 48 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 4
Lecture 49 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 5
Lecture 50 How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 6
Section 14: Stokes law obtained from Navier-Stokes equations
Lecture 51 derivation of Stokes law from Navier Stokes part 1
Lecture 52 derivation of Stokes law from Navier Stokes part 2
Section 15: Appendix on PDE's
Lecture 53 Derivation of the incompressible fluid equation
Section 16: Bonus section: Introduction to the Heisenberg Uncertainty Principle
Lecture 54 Mathematical summary of how to prove the uncertainty principle
Lecture 55 Introduction to the short course on the Heisenberg Uncertainty Principle
Lecture 56 Probability that a particle exists at a certain time
Lecture 57 Probability that a particle has a certain_energy
Lecture 58 Uncertainty in the localization in time and in the energy of the particle
Section 17: Bonus Section: Uncertainty Principle derivation
Lecture 59 Derivation of the uncertainty principle part 1
Lecture 60 Derivation of the uncertainty principle part 2
Lecture 61 Derivation of the uncertainty principle part 3
Section 18: Bonus Section: Consequences of the Uncertainty principle
Lecture 62 Probability that particles come into existence with high energy
Lecture 63 Distribution for which we have the minimum uncertainty
Section 19: Appendix
Lecture 64 Derivation of some formulas used in previous lectures
Students who are interested in Physics and in mathematical derivations of concepts,engineers,mathematicians,physicists,data scientists,computer programmers
Homepage

https://www.udemy.com/course/mathematical-intuition-for-heisenberg-uncertainty-principle/